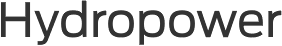Kulekhani hydropower project

The HEC-HMS 3.5 design ended up being always simulate the precipitation runoff procedures of watershed. The areas sub-basins, flow network, alongside basin properties were produced using HEC-GeoHMS and had been later on brought in to HEC-HMS model. The basin model was created making use of deficit and constant loss strategy, Clark product hydrograph, constant monthly base movement and lag techniques. After finishing the basin model, the meteorological model was created utilizing Thiessen polygon gage body weight, made out of HEC-Geo HMS. Thiessen polygons were built based on the rainfall gage point and basin polygon. The Thiessen polygon gage weights for sub-basin were according to three various precipitation programs (for example., Daman, Thankot, Chisapani). The basin average precipitation at each sub-basin had been determined in accordance with Thiessen polygon loads. The model creates the runoff from precipitation considering the topography, earth and landuse qualities, along with the climatic factors like evapotranspiration, and water accessibility within the watershed currently as well as in predicted future climate circumstances ended up being projected. Clark’s product hydrograph model was utilized in the analysis for every single sub-watershed. The machine hydrograph inside strategy is created using the two parameters, time of focus (tc) and storage coefficient (roentgen). The full time of focus means the full time water takes to travel from the farthermost part of the watershed to the watershed socket (Sabol ). HEC-GeoHMS is used for calculation regarding the longest release path. The typical pitch of every sub-watershed and tc were calculated utilizing Kirpich’s formula (Kirpich ). Both tc and R rely on the geography regarding the watershed and they are in range 0.1–500 h and 0–150 h, correspondingly. tc and roentgen had been determined with the next equations (1) and (2), respectively:

$$ {t}_{\mathrm{c}}=\frac{0.0195{(L)}^{0.77}}{S^{0.385}} $$

(1)

in which is the length of the longest release path (m), S the slope of the watershed, and c could be the time of focus (min).The approximation associated with storage coefficient had been made utilizing the after relation derived by Graf et al.:

$$ {\frac{R}{R+t}}_c=\beta $$

(2)

in which β may be the coefficient whoever worth is presumed to be 0.75 for mountainous regions.

The calibration ended up being done to estimate a few of the parameter found in type of HEC-HMS which can not be approximated by observation or dimension of station or watershed traits. Calibration gets better the overall performance of this design. The HEC-HMS rainfall-runoff design inside research ended up being calibrated and validated by evaluating the noticed everyday movement recorded during the inlet associated with the Kulekhani reservoir aided by the flow simulated because of the design. The design calibration had been done utilizing three-year information (1973–1975) and the model had been validated aided by the information for 1977 as discharge data had been readily available till 1978; they certainly were taped for design of Kulekhani hydropower project. The overall performance associated with calibrated and validated model ended up being examined making use of three statistical indices: the coefficient of dedication (R2), the portion amount error (PVE), in addition to Nash-Sutcliffe performance (NSE), that are defined as follows.

The coefficient of dedication (R2) provides the percentage for the variance (fluctuation) of just one adjustable this is certainly foreseeable through the various other variable. The value of R2 differs from 0 (poorest outcome) to at least one (best outcome), with higher values showing less error and, usually, values greater than 0.5 considered acceptable.

$$ {R}^2=\frac{{\displaystyle \sum \Big({Q}_0-\overline{Q_0}}\Big)-\left({Q}_S-{\overline{Q}}_S\right)}{\sqrt{{\displaystyle \sum \Big({Q}_0-\overline{Q_0}}\Big){}^2-{\left({Q}_S-{\overline{Q}}_S\right)}^2}} $$